Cerca de 2700 anos antes de Cristo um cientista egípcio de nome Imhotep, criou o primeiro ciclo zodíaco que ele dividiu em 12 partes iguais. Esse zodíaco marcava o início do ano egípcio quando a estrela Sirius aparecia no céu da cidade de Mênfis, a capital do Império.

Mais tarde os gregos apropriaram se do zodíaco egípcio, dividiram-no em trezentas e sessenta partes, que eles chamaram de graus, e subdividiram esses graus em doze partes, chamadas signos. Os gregos utilizaram suas adaptações para mapear o caminho anual aparente do Sol. Ao medir distâncias, eles criaram o primeiro sistema de referência; era um sistema que tinha um único eixo e que servia como dispositivo para calcular a posição celestial de um planeta expressa em termos de sua distância angular (em graus) até um corpo brilhante qualquer representado, no eixo, por um signo. Essa distância angular foi chamada de Longitude Celestial.

Hiparcchus de Nicéia, introduziu um segundo eixo, que sustentava a distância angular baseada em ângulos retos medidos para o norte ou para o sul de um referencial. O referencial de Hiparcchus foi a linha do horizonte e os ângulos retos eram baseados no zênite do sol a pino. Hiparcchus chamou essa distância angular de Latitude Celestial. Mais tarde, Hipátia de Alexandria, e seu pai Theon, desenvolveriam o sextante para calcular com maior acuidade as latitudes de Hiparcchus. Longitude e latitude celestiais formam o sistema de referência baseado em ângulos oblíquos que é o embrião do sistema que usamos hoje no plano cartesiano.

Ptolomeu chamou essas magnitudes astronômicas de Coordenadas Retangulares e adaptou essas coordenadas para serem usadas no chão. Foi através delas que ele desenhou seus famosos mapas topográficos.

Figura 1: Mapa Mundi de Ptolomeu

Em 380 antes do Cristo Platão lança a obra “A República”, que traz a ideia de separar a Teoria da Prática. Na matemática, isso significou distinguir a ciência pura, a saber: Aritmética e Geometria, da ciência aplicada: música, astronomia, geodesia, óptica, mecânica, logística, etc. Depois os estudiosos Apolônio e Diofanto dedicarem-se a Geometria Analítica.

Por causa dos estudos agora focados no assunto e não na finalidade, surgiu a Exegética na matemática clássica para demonstrar e justificar as descobertas. Exegética era o cálculo de magnitudes aritméticas através de construções geométricas para solucionar equações algébricas.

Viète enquanto estudava Aritmética chamou de Álgebra Geométrica o que antes foi demonstrado por Diofanto usando proposições porísticas ou corolário.

A Geometria Analítica surgiu muito posteriormente com Descartes (1596-1650) no século XVII. Em seu livro O discurso do método, publicado em 1637, Descartes se propõe a encontrar um método capaz de resolver qualquer problema. Numa primeira etapa, ele duvida de todas as coisas e depois procura aquelas verdades que são claras e distintas. Em seguida, procura estudar as coisas desconhecidas comparando-as com as verdades claras e distintas. Como apêndices a O discurso do método, Descartes elabora três aplicações para ilustrar seu método: a geometria, a dióptrica e os meteoros. É em A geometria que Descartes inventa a nova geometria, a Geometria Analítica.

Para Descartes, as verdades claras e distintas, no caso da geometria, são os segmentos que ele, como os gregos anteriormente, identifica com os números. Na consideração de um certo problema, diz ele, devemos escrever a equação que liga os segmentos conhecidos aos desconhecidos e a partir delas resolver os problemas. Ele observa que a geometria é “difícil” e a álgebra “fácil”, e que seu método, nesse caso, se limitava a resolver os problemas difíceis que os gregos haviam proposto pela álgebra, mais clara e fácil de manipular.

Exemplo 1: Considere as rectas dadas pelas equações

y = x e y = x + 1

Estamos interessados nos pontos do plano que satisfazem simultaneamente as duas equações. Substituindo a primeira equação na segunda temos x = x + 1 e logo 1 = 0! Logo, as duas equações não possuem soluções em comum. Nesse caso, a tradução que Descartes procurava da álgebra para a geometria é que a ausência de soluções em comum significa que as rectas são paralelas. Veja a Figura 2.

Percursores da geometria analítica

Menaecmo

Menaecmo nasceu em Alopeconeso, na Trácia em 380 a.C. e morreu em Cízico na Mísia em 320 a.C.. Ele foi aluno de Eudoxo, portanto era discípulo da Escola Pitagórica. Enquanto seu irmão, Dinostrato, se dedicou a enquadrar o círculo, Menaecmo prestou atenção a outro problema grego clássico: o Problema Deliano da duplicação do cubo.

Para conseguir a medida do novo cubo de volume dobrado em relação ao cubo original de lado um, Menaecmo utilizou duas curvas conhecidas dos geómetras gregos, mas que, até então, não tinham sido de muita utilidade: a hipérbole e a parábola. O motivo pelo qual Menaecmo é considerado o introdutor das Seções Cônicas é que, até ele, as curvas eram meras construções geométricas sem representação algébrica, além disso, na resolução do problema Deliano, intersecionar hipérbole e parábola, ele acabou descobrindo uma terceira curva: a elipse.

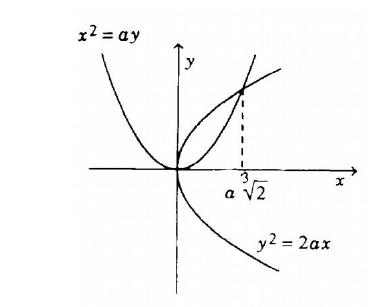
O que ele fez foi usar as proporções de Eudoxo para algebrizar uma hipérbole conveniente em y²=2ax e uma parábola adequada em y=x²/a; ao resolver o sistema entre as duas equações ele descobriu um ponto cuja menor distância a origem do sistema de referência utilizado era exactamente a medida desejada para o lado do novo cubo (que hoje dizemos ser a raiz cúbica de dois, impossível de se obter na época apenas com régua e compasso).

Figura 2: A Resolução de Menaecmo da Duplicação do Cubo

Apolônio

Apolônio de Perga nasceu em Perga na Panfília em 262 a.C. e morreu em Alexandria no Egito em 190 a.C.. Apolônio ficou conhecido por seus contemporâneos como “O Grande Geômetra” a Apolônio era matemático de muitas faces e também foi astrônomo respeitado, mas certamente sua obra prima foi as “Cônicas”. Nessa obra, escrita originalmente em oito livros, dos quais só se tem registro dos sete primeiros, Apolônio recapitula os conceitos conhecidos das seções, mas amplia-os enormemente. Por exemplo, foi Apolônio quem instituiu o cone de folha dupla; ele provou que as seções podem ser obtidas a partir de cones oblíquos; ele também provou que de um único cone pode-se obter as três cônicas bastando variar a inclinação do corte; e finalmente foi ele quem oficializou a nomenclatura atual, baseando-se nas relações entre um quadrado sobre as ordenadas – y² – e um retângulo sobre a abcissa “x” e o latus rectum “l” – lx – assim:

Parabola (comparação): y² = lx

Hyperbola (lançamento além): y² > lx
Ellipsis (falta): y² < lx

Apolônio, limitado que era pela notação da época, ainda instituiu as formas canônicas das equações das cônicas:

Parábola: y² = 2px
Hipérbole: x²/a² - y²/b² = 1
Elipse: x²/a² + y²/b² = 1

despeito de o título hoje ser auferido a Euclides.

Diofanto

Pouco se sabe da vida de Diofanto exceto que ele viveu em Alexandria e quantos anos ele viveu por conta de uma charada em sua lápide (resolvida a charada ele teria vivido 84 anos). Alguns historiadores recentemente consideram que ele deve ter vivido durante o século III da era cristã por causa de referências de autores da época, como Teão, pai de Hipatia, e de referências feitas pelo próprio Diofanto em sua obra citando autores contemporâneos como Hipsícles.

Em fim, indiferente de seu local de nascimento e morte, nos interessa sua vida, e Diofanto é respeitado como “Pai da Álgebra” clássico por sua obra “Aritmética” em que trata basicamente de Teoria dos Números e equações algébricas, abrindo caminho para uma notação muito mais manuseável, ponto de virada para o estudo da Geometria Analítica, em suas equações diofantinas.

Esse tipo de equação é muito debatida porque uma tradução da “Aritmética”, feita por Bachet no século XVI, foi lida por Pierre de Fermat que, em suas margens, diz ter conseguido uma solução simples para uma equação diofantina que ficaria conhecida como “O Último Teorema de Fermat”, mas que não poderia mostra-la devido à limitação da dita margem.

Xⁿ + Yⁿ = Zⁿ

Viète e Ghetaldi

François Viète nasceu em Fontenay-le-comte em 1540 e morreu em Paris em 1603, na França. Marino Ghetaldi nasceu em 1568 e morreu em 1626 numa cidade da Dalmácia chamada Ragusa, hoje Dubrovnik na Croácia. Os dois eram advogados, mas nenhum dos dois passou muito tempo na legislatura. Ambos tornaram-se matemáticos amadores muito respeitados.

Durante os séculos XVI e XVII, estava muito na moda traduzir obras clássicas. Por ser huguenote Viète foi exilado algumas vezes e, durante seus exílios, se dedicou a traduzir as obras de Apolônio. Essas traduções lhe renderam conhecimento suficiente para publicar uma obra original intitulada In artem analyticam isagoge que lhe rendeu a alcunha de “Pai da Álgebra” moderno.

Nesse livro, ele trata de equações de 2º, 3º e 4º graus e revoluciona a simbologia existente criando uma notação muito parecida com a de que dispomos hoje; por exemplo, foi ele quem sugeriu que letras fossem usadas para quantidades, quer fossem conhecidas ou desconhecidas: para as desconhecidas, ele designou as primeiras letras do alfabeto, para as conhecidas, as últimas. Foi ele também que sugeriu o nome coeficiente para as magnitudes conhecidas. Viète só não disse a última palavra com relação à notação moderna porque ele não concebia a heterogeneidade de dimensões.

Ghetaldi aparece como continuador e discípulo de Viète por tê-lo conhecido num dos exílios do mestre e se interessado pelas traduções em que o francês se empenhava. Vale lembrar que Viète morreu antes de poder concluir suas traduções e foi Ghetaldi quem assumiu a responsabilidade de termina-las.

Da mesma forma que aconteceu com seu antecessor, Ghetaldi se envolveu tanto nas traduções que acabou escrevendo sua própria obra, nela um livro intitulado De resolutione et de compositione mathematica, libri quinque em que ele utiliza a simbologia de Viète para estender seu trabalho e elucidar a homogeneidade de dimensões de que seu mentor era tão fã.

Esse livro foi a inspiração para aquele que viria a ser a maior referência da Geometria Analítica: René Descartes.

Descartes

René Descartes nasceu em La Haye na França em 1596 e morreu em Estocolmo na Suíça em 1650. Era advogado formado pela Universidade de Poitiers, mas formou-se apenas para satisfazer seu pai. De fato, assim que recebeu o diploma ele o entregou ao pai e saiu de casa para alistar-se como militar voluntário do exército de Maurício de Nassau em 1616. Durante os doze anos seguintes, ele peregrinou pela Europa estudando tudo o que lhe caia nas mãos.

Descartes foi um grande filósofo no sentido mais amplo da palavra, ele era um “amigo do conhecimento”. As conquistas de Descartes na Geometria Analítica são, ao mesmo tempo, superestimadas e subestimadas. São superestimadas porque nada, nem mesmo o plano que leva seu nome (cartesiano), foi ideia originalmente dele, se muito podemos dizer que ele reconfigurou conhecimentos muito mais antigos. Elas são também subestimadas porque não são reconhecidas pelo que realmente são: tudo que Descartes fez na Geometria Analítica foi do ponto de vista de um professor, não de um matemático. É claro que ele tinha conhecimentos matemáticos profundos, mas sua real contribuição reside na didática em ensinar esses conhecimentos.