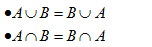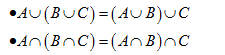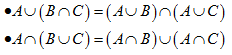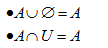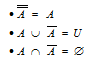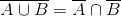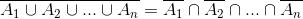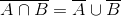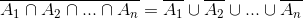
Fechamento
Quaisquer que sejam os conjuntos A e B, a reunião de A e B, denotada por A U B e a interseção de A e B, denotada por A B, ainda são conjuntos no universo.
Comutatividade
Quaisquer que sejam os conjuntos A e B, tem-se que:
Associatividade
Quaisquer que sejam os conjuntos A, B e C, tem-se que:
Distributividade
Quaisquer que sejam os conjuntos A, B e C, tem-se que:
Propriedades do Elemento Neutro
O conjunto vazio Ø é o elemento neutro para a reunião de conjuntos. E a interseção do conjunto vazio Ø com qualquer outro conjunto A, fornece o próprio conjunto vazio. Assim qualquer que seja o conjuntos A, tem-se que:
Propriedades do complemento
Assim qualquer que seja o conjuntos A, tem-se que:
Leis de Augustus De Morgan
Augustus De Morgan foi matemático e professor indiano radicado na Inglaterra, um dos fundadores da BAAS (British Association for the Advancement Science). Nasceu em 1806 na Índia e com sete meses de idade foi para a Inglaterra com a família. Em 1830 publicou o livro Elements of Arithmetic. Em 1831 ajudou a fundar a BAAS. Em 1838 publica o artigo Induction no qual é introduzido o conceito de indução matemática. Em 1849 trigonometry and double álgebra, na qual ele fornece uma interpretação geométrica para os números complexos.
Juntamente com George Boole, Augustus De Morgan, tornou-se um dos responsáveis pela criação da lógica simbólica moderna.
Definição de complementar de um conjunto
Dado o conjunto Universal U e um subconjunto A. Chama-se complementar do conjunto A e expressa-se por C(A) a todos os elementos do Universo que não fazem parte do conjunto A.
Leis de Augustus De Morgan (Complementos de conjuntos)
- O complementar da reunião dos conjuntos A e B é a interseção dos complementares desses conjuntos.
2. O complementar da reunião de uma coleção finita de conjuntos é a interseção dos complementares desses conjuntos.
3. O complementar da interseção dos conjuntos A e B é a reunião dos complementares desses conjuntos.
4. O complementar da interseção de uma coleção finita de conjuntos é a reunião dos complementares desses conjuntos.