Um conjunto é uma coleção de elementos.
Exemplos:
- conjunto dos dias da semana: 2ª feira, 3ª feira, 4ª feira, 5ª feira, 6ª feira, sábado, domingo
- conjunto de vogais do alfabeto português: a, e, i, o, u
Os símbolos têm uma grande importância na nossa vida. Também em Matemática se usa linguagem simbólica para facilitar a comunicação.
Para melhor simplificação de linguagem escrita e oral vamos designar os conjuntos por letras maiúsculas (A, B, C, D, . . .) e os elementos por letras minúsculas (a, b, c, d, . . .).
Há conjuntos com designação especial:
IN – conjunto dos números naturais
Q – conjunto dos números racionais
IR – conjunto dos números reais
Formas de definição de conjuntos
Por Compreensão:
Na definição de um conjunto por compreensão coloca -se entre chavetas uma propriedade comum dos elementos do conjunto (no plural e com letra minúscula).
A = {números naturais menores de 6}
Por Extensão:
Quando se enumera todos os elementos do conjunto escrevendo-os entre chavetas e separando-os por virgulas.
A = {0, 1, 2, 3, 4, 5}
Por meio de chavetas
Na representação por chavetas os elementos são separados por virgulas
A={ 0 , 1 , 2 , 3 , 4 , 5 }
B={ retângulo, quadrado, losango , trapézios}
Por meio de diagrama de Venn:
Relação de pertença e não pertença
Um elemento pode pertencer ou não a um determinado conjunto. Para se indicar que um elemento pertence a um dado conjunto, utilizamos o símbolo e quando não pertence usamos .
x A ( lê-se: x pertence a A)
x B ( lê-se: x não pertence a B)
Exemplos:
Linguagem corrente | Linguagem simbólica |
2 é um número par | 2 {números pares} |
2 não é um número ímpar | 2 { números ímpares} |
Sérgio é um elemento da turma A | Sérgio A |
Conjunto singular e conjunto vazio
Conjuntos singulares são conjuntos que têm apenas um elemento.
Exemplos: A = {0}, B = {a}, B = {Lucas}
Conjuntos vazios são aqueles que não têm nenhum elemento. E representa-se por: {} ou Ø.
Exemplos: A = {}, B = {}, B = {}
Subconjunto
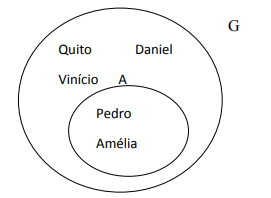
Seja G o conjunto dos alunos dum grupo duma turma do 1º ano do IFP.
O conjunto A é parte do conjunto G porque todos os elementos de A pertencem a G.
Diz-se então que A é subconjunto de G.
Nota:
- Qualquer conjunto é subconjunto de si próprio
- O conjunto vazio é subconjunto de qualquer conjunto.
Cardinal de um conjunto - Notação: #
Chama-se cardinal de um conjunto e representa-se pelo símbolo #, ao número de elementos desse conjunto.
Exemplos:
A = {2, 4, 6, 8, 10}, #A = 5
B = {números dígitos}, #B = 10