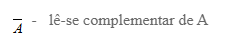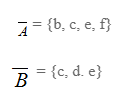
Conjunto universal ou universo

Chama-se Conjunto Universal (ou Universo) ao conjunto constituído por todos os elementos do universo considerado.

Exemplos:  R = {números reais}

A = {alunos da minha turma}

Relação de inclusão

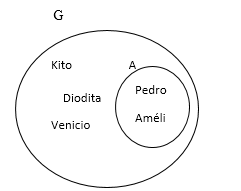
Repara no diagrama seguinte que o conjunto A é parte do conjunto G porque todos os elementos de A pertencem ao conjunto G.

Diz-se então que  A é subconjunto de G ou que  A está contido em G.

 Porque nem todos os elementos de P pertencem a G, diz-se que o conjunto P não está contido no conjunto G.

Reunião de dois conjuntos

1. Consideremos dois conjuntos A e B:

A={ a, b, c}                               

B={m , p}

O conjunto formado por elementos dos dois conjuntos chama-se conjunto reunião de A e B. Escreve-se A U B                                                            

U – lê-se “reunião”

Assim, A U B = {a, b, c, m, p}

Considera agora os conjuntos C e D

 C = {a, b, c, d}                         

 D = {a, m, c, p, t}

O conjunto reunião de C e D é C U D = {a, b, c, d, m, p, t}              

Ao formar o conjunto reunião os elementos comuns não devem ser repetidos.

Intersecção de conjuntos 

Considere conjunto A de números naturais menores de 6

A = {0, 1, 2, 3, 4, 5}

E o conjunto B de múltiplos de 2 menores de 10.

B = {0, 2, 4, 6, 8}

Ao conjunto {0, 2, 4} formado pelos elementos comuns aos dois conjuntos, chamamos conjunto intersecção de A com B e representa-se por ∩ .

Assim, A ∩ B = {0, 2, 4}    

Conjuntos disjuntos

Observa os conjuntos A = {a, b, c}     e        B = {1, 2, 3}.

A intersecção destes conjuntos é:

 A ∩  B = Ø     ou        A ∩ B = {  }.

Se a intersecção de dois ou mais conjuntos é um conjunto vazio diz-se que eles são conjuntos disjuntos.

Exemplo:

Os conjuntos A e B são conjuntos disjuntos.

Diferença entre dois conjuntos

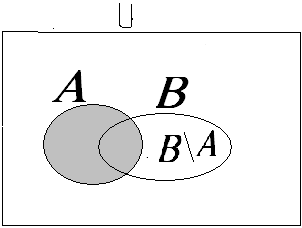
Dados dois conjuntos A e B, chama-se diferença de A e B, denotada por A - B ou A\B,  o conjunto que contém aqueles elementos que estão em A mas não estão em B.

B\A - lê-se B menos A

Se A = {a, b, c, d, e, f} e B = {a, d, g, h, m, n}, então:

A / B = {b, c, e, f}                   

 B/A = {g, h, m, n}

Complementar de um conjunto

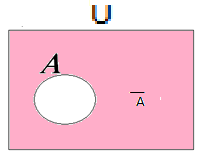
Dado o conjunto Universal U e um subconjunto A. Chama-se complementar do conjunto A e expressa-se por C(A) a todos os elementos do Universo que não fazem parte do conjunto A.

 C(A)  -   lê-se complementar de A , ou

Exemplo:

Dados o conjunto U e os subconjuntos A e B, assim definidos:

U = {a, b, c, d, e, f, g}                  

A= {a, d, g};               

B = {a, b, f, g}

Observa: